Wobble, the Two-Wheel Self-Balancing Robot
Simulation Demo
I created a barebones URDF that resembled the self balancing robot I was going to build and threw it in PyBullet. I created a simulation script that would allow me to send control signals to each of the robot's wheels. I also set "limits" to how fast the robot's wheels were able to turn.
For each controller, I ran 3 trials and considered them successful if the robot was able to balance for at least 5 seconds. This was one of my success critera in my project proposal. Each simulation was initialized with the same random seed. To mimic sensor noise, I added uniform noise (+/- 0.5) to the pitch reading, which was then fed into the controller. Additionally, to mimic inconsistencies in each motor's output, I added more uniform noise to each controller signal (+/-) 2 to the left wheel, and (+/-) 1 to the right wheel.
Each recorded demo below is Trial 1.
PID Control (P=10, I=100, D=0)
Tuning the PID controller was kind of intuitive, as I realized the robot needed to be aggresive in it's corrections (high I-gain). Through trial and error I learned that adding any damping (increased D-gain) would cause the robot to eventually fall, as it would be slowing down its corrective step.
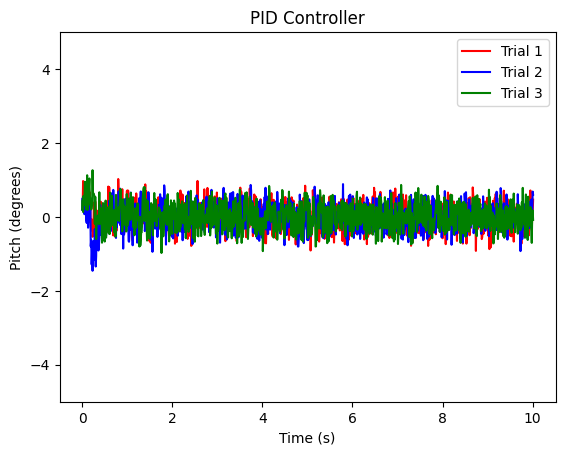
Average latency to compute control signal: 2.012 microseconds
Linear Quadratic Regulator (LQR) Control
LQR was a bit trickier to implement compared to PID, as it required a mathematical model of the system to control. When I created my URDF file I wasn't really thinking about this part. In fact, I used PyBullet+URDF to avoid the mathematical model part. After trying random A, B, Q, R matricies to no avail, I turned to black box system identification. Basically, to make an approximation of the system's dynamics, I was going to set the robot at different pitches, and input some random control signal. Then I would see how the robot responded and fit to a linear model using least squares regression. After that, I did a basic grid search to find decent Q and R matrices and were able to get decent results as seen by the demo below.
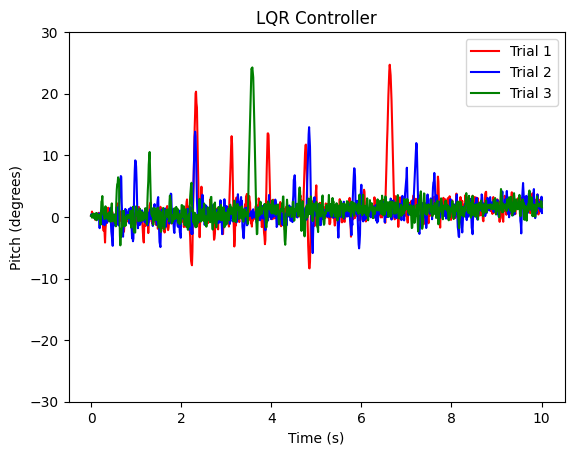
Average latency to compute control signal: 7.450 microseconds
Model Predictive Control (MPC)
MPC was similar to LQR in that it shared a similar A, B, Q, and R matrix. However, it had an extra parameter because it required to optimized across a horizon, N. Through a simple script I made, I tried every N and sorted them by the RMSE of the pitch across the entire run. I found that using N=3 was good enough to get it to balance for 10 seconds.
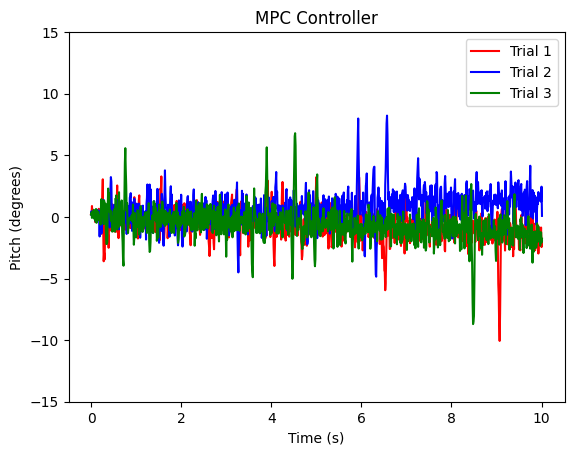
Average latency to compute control signal: 677.376 microseconds
Trial and Error
Failure 1: I suspected that my robot was oscillating a lot due to poor PID gains. Additionally, there was some presence of steady state error when eventually caused the robot to tip over past a certain threshold.
Improvement: Compensate for weak motors by increasing the diameter of wheels from 8.8cm to 13cm.

Autonomous Demo
After increasing the wheels and modifying the PID values, I was able to successfully balance the robot for over 5 seconds, and have it continue to balance when external forces were applied. My final PID values were P=10, I=12, and D=0.4.